Действия с отрицательными и положительными числами
Абсолютная величина (модуль).
Сложение.
Вычитание. Умножение. Деление.
Абсолютная величина (
модуль
).
Для отрицательного числа – это
положительное число, получаемое от перемены его знака с « – » на « + »; для
положительного числа и нуля – само это число. Для обозначения
абсолютной величины (модуля) числа используются две прямые черты, внутри которых
записывается это число.
П р и
м е р ы :
|
– 5 | = 5, | 7 | = 7, | 0 | = 0.
| Сложение: |
1) при сложении двух чисел с
одинаковыми знаками складываются
их абсолютные величины и
перед суммой ставится общий знак.
П р и м е р ы :
( + 6 ) + ( + 5 ) = 11 ;
( – 6 ) + ( – 5 ) = – 11 .
2) при сложении двух чисел с
разными знаками их абсолютные
величины вычитаются ( из
большей меньшая ) и ставится знак
числа с большей абсолютной
величиной.
П р и м е р ы :
( – 6 ) + ( + 9 ) = 3 ;
( – 6 ) + ( + 3 ) = – 3 .
|
Вычитание.
Можно заменить вычитание двух чисел
сложением, при этом уменьшаемое сохраняет свой знак, а вычитаемое берётся с
обратным знаком.
П р и м е р ы :
( + 8 ) – ( + 5 ) = ( + 8 ) + ( – 5 ) = 3;
( + 8 ) – ( – 5 ) = ( + 8 ) + ( + 5 ) = 13;
( – 8 ) – ( – 5 ) = ( – 8 ) + ( + 5 ) = – 3;
( – 8 ) – ( + 5 ) = ( – 8 ) + ( – 5 ) = – 13;
Умножение.
При умножении двух чисел их абсолютные
величины умножаются, а произведение принимает знак « + » , если знаки
сомножителей одинаковы, и знак « – » , если знаки сомножителей разные.
Полезна следующая схема (правила
знаков при умножении):
+
·
+ = +
+
·
– = –
–
·
+ = –
–
·
– = +
При
умножении нескольких чисел (
двух и более
)
произведение имеет знак «
+
»
,
если число отрицательных сомножителей чётно, и знак «
–
»
,
если их число нечётно.
П р и м е р :
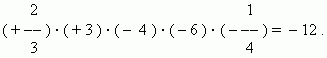
Деление.
При делении двух чисел абсолютная
величина делимого делится на абсолютную величину делителя, а частное принимает
знак
«
+
»
, если знаки делимого и
делителя одинаковы, и знак
« – »
, если знаки делимого и
делителя разные.
Здесь действуют те же
правила знаков, что и при умножении:
+
:
+ = +
+
:
– = –
–
:
+ = –
–
:
– = +
П р и
м е р :
( – 12 ) : ( + 4 ) = – 3 .
| 




