Деление многочленов
Что значит разделить один многочлен
P
на другой Q
? Это значит найти многочлены М (частное) и
N
(остаток), удовлетворяющие двум требованиям:
1) имеет место равенство:
MQ
+ N
= P
;
2) степень многочлена
N
меньше степени многочлена Q.
Деление многочленов
может быть выполнено по следующей схеме:
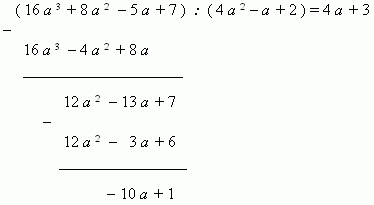
1) Делим первый член 16a³
делимого на первый член 4a²
делителя;
результат
4a
является первым членом частного.
2)
Умножаем полученное
выражение 4a на делитель 4a²
– a
+ 2 ;
записываем
результат 16a³
– 4a²
+ 8a
под делимым (один подобный
член под другим).
3)
Вычитаем
почленно этот результат из делимого и сносим вниз
следующий по
порядку член делимого 7; получаем
остаток
12a²
–13a
+ 7 .
4) Делим первый член 12a²
этого
выражения на первый член 4a²
делителя; результат 3 – это второй член частного.
5) Умножаем этот
второй
член частного 3 на делитель
4a²
– a
+ 2 и вновь
записываем результат 12a²
– 3a
+ 6 под делимым (один
подобный член под другим).
6) Вычитаем почленно
полученный результат из предыдущего остатка и получаем
второй остаток: – 10a
+ 1. Его степень меньше
степени делителя, поэтому деление заканчивается.
В результате получили частное 4a
+
3 и
остаток –10
a
+
1.
| 




