Каталог статей

Некоторые виды уравнений высших степеней можно решить, используя квадратное уравнение. Иногда можно разложить левую часть уравнения на множители, каждый из которых является многочленом не выше второй

степени. Тогда, приравнивая каждый из них к нулю и решая все эти квадратные и / или линейные уравнения, мы получим все корни исходного уравнения.

П р и м е р .  Решить уравнение:  3x ⁴ + 6x ³ – 9x ²  = 0 .

Р е ш е н и е .  Разложим левую часть этого уравнения на множители:

                                                         x ² ( 3x ²  +  6x –  9 ) .

                         Решим уравнение:  x ² = 0; оно имеет два корня: x₁ = x₂ = 0 .

                         Теперь решим уравнение: 3x ² + 6x – 9 = 0,  и получим:

                         x₃ = 1  и  x₄ = – 3 .

                         Таким образом, исходное уравнение имеет четыре корня:

                         x₁ = x₂ = 0 ;   x₃ = 1 ;   x₄ = – 3 .

Если уравнение имеет вид:

                                                          ax²ⁿ + bxⁿ +  c = 0  ,

оно приводится к квадратному уравнению заменой:

                                                               xⁿ = z ;

действительно, после этой замены получаем:   az ²+ bz + c = 0 .

П р и м е р .  Рассмотрим уравнение:

                                                        x ⁴ – 13 x ² + 36 = 0 .

                       После замены:  x ² = z  получим уравнение:                                                       

                                                                                   z ² – 13 z + 36 = 0 .

                       Его корни:  z₁ = 4  и  z₂ = 9. Теперь решаем  уравнения:                                                                   

                              x ² = 4  и  x ² = 9 . Они имеют соответственно корни:

                       x₁ = 2 ,  x₂ = – 2 ,   x₃ = 3 ;   x₄  = – 3 .  Эти числа являются

                       корнями исходного уравнения ( проверьте, пожалуйста! ).

Любое уравнение вида:  ax ⁴ + bx ² + c = 0  называется биквадратным.

Оно приводится к квадратному уравнению заменой:

                                                          x² = z .                                                                                                         

П р и м е р .  Решить биквадратное уравнение:  3x ⁴ – 123x ² + 1200 = 0 .

Р е ш е н и е .  Заменяя:  x ² = z ,  и решая уравнение:

                         3z ² – 123z + 1200 = 0, получаем: 

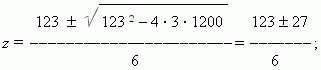
                         отсюда,  z₁ = 25 и  z₂ = 16. Используя нашу замену, получим:

                          x ² = 25 и  x ² = 16,  отсюда,  x₁ = 5,  x₂ = – 5,  x₃ = 4,  x₄ = – 4.