Иррациональные числа.
Формула сложного радикала
Рациональные
числа. Иррациональные числа.
Примеры иррациональных чисел.
Формула
сложного радикала.
Иррациональные числа
в отличие от рациональных (см. “Рациональные числа”)
не могут быть представлены в виде обыкновенной несократимой дроби вида:
m
/
n, где
m и
n – целые числа. Это числа нового типа, которые
могут быть вычислены с любой точностью, но не могут быть заменены рациональным
числом. Они могут появиться как результат геометрических измерений, например:
- отношение длины диагонали квадрата к длине его стороны равно
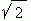 , ,
- отношение длины окружности к длине её диаметра равно иррациональному числу

Примеры других иррациональных чисел:
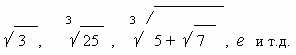
Докажем, что
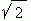 является
иррациональным числом. Предположим противное: является
иррациональным числом. Предположим противное:
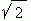 -
рациональное число, тогда согласно определению рационального числа можно
записать: -
рациональное число, тогда согласно определению рационального числа можно
записать:
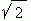 =
m
/ n
, отсюда: 2 =
m2
/ n2,
или m2 =
2 n2,
то есть m2 делится на 2, следовательно, m
делится на 2, откуда
m
= 2 k,
тогда m2
= 4 k2 или 4
k2
= 2 n2,
то есть n2 = 2
k2,
то есть n2 делится на 2, а значит, n
делится на 2, следовательно, m
и
n имеют общий множитель 2, что противоречит
определению рационального числа (см. выше). Таким образом, доказано, что =
m
/ n
, отсюда: 2 =
m2
/ n2,
или m2 =
2 n2,
то есть m2 делится на 2, следовательно, m
делится на 2, откуда
m
= 2 k,
тогда m2
= 4 k2 или 4
k2
= 2 n2,
то есть n2 = 2
k2,
то есть n2 делится на 2, а значит, n
делится на 2, следовательно, m
и
n имеют общий множитель 2, что противоречит
определению рационального числа (см. выше). Таким образом, доказано, что
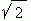 является
иррациональным числом. является
иррациональным числом.
При алгебраических
преобразованиях иррациональных выражений и уравнений, содержащих квадратные
корни, может быть полезна следующая формула сложного радикала:
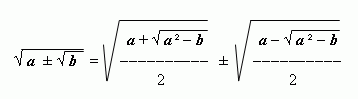
(все подкоренные выражения неотрицательны). Для
доказательства этой формулы достаточно возвести в квадрат обе ее части.
| 




