Действия с обыкновенными дробями

Расширение дроби. Сокращение дроби. Сравнение дробей.

Приведение к общему знаменателю. Сложение и вычитание дробей.

Умножение дробей. Деление дробей.

Расширение дроби. Значение дроби не меняется, если умножить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется расширением дроби. Например,

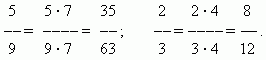
Сокращение дроби. Значение дроби не меняется, если разделить её числитель и знаменатель на одно и то же число, отличное от нуля. Это преобразование называется сокращением дроби. Например,

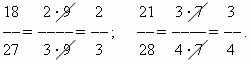
Сравнение дробей. Из двух дробей с одинаковыми числителями та больше, знаменатель которой меньше:

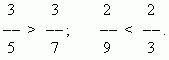
Из двух дробей с одинаковыми знаменателями та больше, числитель которой больше:

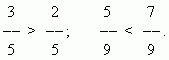
Для сравнения дробей, у которых числители и знаменатели различны, необходимо расширить их, чтобы привести к общему знаменателю.

П р и м е р .  Сравнить две дроби:

 

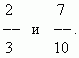
Р е ш е н и е.

Расширим первую дробь на знаменатель второй, а вторую - на знаменатель первой:

Использованное здесь преобразование называется приведением дробей к общему знаменателю.

Сложение и вычитание дробей. Если знаменатели дробей одинаковы, то для того, чтобы сложить дроби, надо сложить их числители, а для того, чтобы вычесть дроби, надо вычесть их числители (в том же порядке). Полученная сумма или разность будет числителем результата; знаменатель останется тем же. Если знаменатели дробей различны, необходимо сначала привести дроби к общему знаменателю. При сложении смешанных чисел их целые и дробные части складываются отдельно. При вычитании смешанных чисел мы рекомендуем сначала преобразовать их к виду неправильных дробей, затем вычесть из одной другую, а после этого вновь привести результат, если требуется, к виду смешанного числа.

П р и м е р .

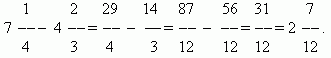
Умножение дробей. Умножить некоторое число на дробь означает умножить его на числитель и разделить произведение на знаменатель. Следовательно, мы имеем общее правило умножения дробей: для перемножения дробей необходимо перемножить отдельно их числители и знаменатели и разделить первое произведение на второе.

П р и м е р .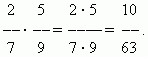

Деление дробей. Для того, чтобы разделить некоторое число на дробь, необходимо умножить это число на обратную дробь. Это правило вытекает из определения деления (см. раздел “Арифметические операции”).

П р и м е р .
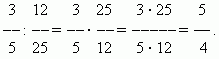