Задачи в стихах
Не секрет, что учащиеся
часто воспринимают физику как науку сухую,
скучную. Действительно, часто ли на уроке мы
находим время для шутки? И стоит ли удивляться,
что бесконечно повторяющиеся в задачах «тележки
с грузом» и «шарики на нитях» внушают многим
ученикам, особенно с ярко выраженными
гуманитарными способностями, стойкую неприязнь?
Вот почему я активно ввожу в практику задачи в
стихах. Такая форма подачи материала делает
поиск ответа делом увлекательным. Эти задачи
можно использовать во внеклассной, кружковой
работе, при проведении факультативных занятий,
при оформлении стендов. Стихи, конечно, не
назовёшь безупречными, но ребятам решать
рифмованные задачи нравится.
1. Карандаш в графине
В графин с водою карандаш 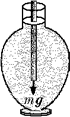
Мальвина уронила.
«Карандаш не утонул, –
Заметил Буратино. –
Погрузился карандашик
На три четверти всего!»
А теперь скажи, какая
Была плотность у него?
Решение а
На уровне основания карандаша
его вес равен весу вытесненной воды: Рк
= Рв. Запишем:
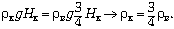
Решение б
Карандаш находится в
состоянии равновесия, значит, сумма сил,
действующих на карандаш, равна нулю. В проекции
на ось Y:
FA – mg = 0 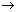 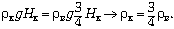
Ответ. 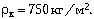
2. Дед Мазай на рыбалке
Дед Мазай рыбачил с лодки.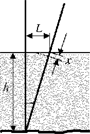
Чтоб измерить глубину,
Отклонил он на полметра
В реке тростиночку одну.
На ладонь тростинка эта
Погрузилась в бездну вод,
А теперь скажите: можно ль
Перейти ту речку вброд?
Сделаем чертёж. Обозначим: h –
глубина реки, L – отклонение тростинки, Х
– глубина погружения. Для получившегося
прямоугольного треугольника запишем теорему
Пифагора:
(h + X)2 = L2 + h2
и решим полученное уравнение: 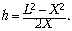
Ответ. h = 1,5 м.
3. Оптический обман
Купила мама Лёшке
Отличные сапожки –
Восемь дюймов высотой
И с подошвою литой.
В них Алёше целый день
Лужи измерять не лень.
Ворчала мама: «Ай-ай-ай,
Ведь залилось же через край!»
В чём же Лешина вина?
Казалась меньше глубина!
Решение
Введём обозначения: Н –
истинная глубина лужи, h – кажущаяся глубина
лужи, n – показатель преломления воды.
Запишем закон преломления света: 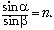 Так как Так как 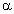 мало, то sin мало, то sin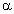 = tg = tg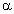 . Следовательно, . Следовательно,
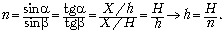
Ответ. h = 6 дюймов 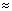 15 cм. 15 cм.
4. Сбор металлолома
Смастерили лодку
Весёлые дружки,
Чтоб собрать
металлолом
В порту со дна реки,
На лодку извели они
Три тонны чугуна...
А водоизмещением
В пять тонн у них она.
Якорь с цепью
в сто пудов –
Хорошая находка.
Да не потянет ли на дно
За собой он лодку?
Решение
Водоизмещение судна – это вес
воды, вытесненной судном при погружении до
ватерлинии. А у плавающего тела вес вытесненной
воды равен весу тела: Рводы = Рсудна+
Ргруза. Из условия задачи видно, что
водоизмещение больше, чем вес лодки с грузом,
лодка останется на плаву, если в ней кроме якоря с
цепью будет не более 400 кг груза.
5. Новогодняя
Зеркальный шар-серьга упал
У ёлочки с «уха».
На осколок вскоре села
Муха-Цокотуха.
Себе в сфере показалась
Вдвое увеличенной,
Над собой расхохоталась
Аж до неприличия!
Взлёт, посадка – перед нею
Сторона обратная.
Какой себя увидала?
Вот задачка знатная.
Решение
Понятно, что Муха-цокотуха
сначала села на внутреннюю поверхность
зеркального осколка (вогнутого зеркала). Её
изображение было мнимым. Запишем уравнение
сферического зеркала: 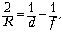 где R – радиус шара, d – раccтояние
от глаз мухи до полюса зеркала, f – расстояние
до изображения. Знак «–» перед f означает, что
изображение мнимое. Увеличение в данном случае: где R – радиус шара, d – раccтояние
от глаз мухи до полюса зеркала, f – расстояние
до изображения. Знак «–» перед f означает, что
изображение мнимое. Увеличение в данном случае: 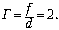
Во второй ситуации зеркало
выпуклое, уравнение сферического зеркала: 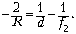
Увеличение 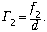
Решая совместно полученные
равенства, получим 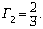
Ответ. Муха увидела себя
уменьшенной на треть.
6. Очки
В дневник мой папа, сняв очки,
Глядит с протянутой руки.
А ну-ка, дети, оцените,
Какие у него очки?
А у меня что за очки,
Коли, на папины сменив их,
Я вижу самый мелкий шрифт,
Когда листок на дециметр
От носа отодвину?
Примем длину руки d = 0,75 м,
расстояние наилучшего зрения d0 = 0,25
м, расстояние, заданное в условии, d1 = 0,1
м. Обозначим оптическую силу глаза через D,
оптическую силу очков D0, расстояние от
линзы очков до сетчатки глаза f.
Запишем формулы:
для чтения без очков: 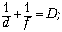
для чтения в очках: 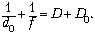
Решая совместно оба уравнения,
получим:
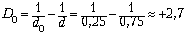 (дптр). (дптр).
Для решения второй части
задачи введём обозначения: f – расстояние от
линзы до сетчатки глаза, Dг –
оптическая сила глаза, Dп – оптическая
сила папиных очков, Dс – оптическая
сила своих очков. Запишем формулы:
в папиных очках: 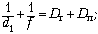
в своих очках: 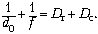
Решая совместно два последних
уравнения, получим Dс = –3,3 дптр.
7. Пошёл однажды Витёк
купаться. Пока собрался, пока до речки дошёл –
солнышко уже высоко поднялось, на две трети
прямого угла. А водичка чистая, прохладная, так и
тянет нырнуть, понежиться в прохладной глубине.
Время незаметно летит, да и замёрз уже. Нырнул в
последний раз, зацепился руками за корягу на дне
и посмотрел из-под воды вверх на солнышко, а оно
опять на той же высоте – две трети прямого угла!
Пора домой бежать!
Сколько времени купался Витёк?
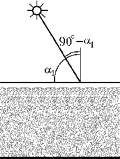
Решение
Запишем закон преломления для
солнечных лучей, попадающих в глаз наблюдателя,
находящегося на дне:
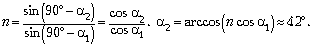
Стало быть, Земля за время
купания повернулась вокруг своей оси на угол 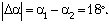
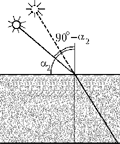
На 360° Земля повернётся за 24 ч.
Время купания найдём из пропорции: 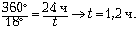
«Нельзя писать на белом
мелом», –
Пытались мне растолковать.
Писать-то можно, но, однако,
Написанного не видать…
|
Источник: http://fiz.1september.ru | 




